Randomblind issuance

Randomblind attributes are a new IRMA feature introduced in irmago v0.6.0 that can give the user extra privacy guarantees during issuance. Specifically, if this mode of issuance is enabled for an attribute within a credential type, this attribute is guaranteed to

1. be random, i.e., unequal to all previously issued instances of this attribute and
2. remain unknown to the issuer, while it still signs the attribute as part of the credential.

Note that the latter property holds up until a user decides to disclose the attribute. In this sense, the attribute can be seen as a one-time attribute.

This page explains how to enable this feature and later how this guarantee is upheld cryptographically. The primary use case of this feature is online voting, where voting secrecy plays a vital role. In the last section, we will explain how randomblind attributes can be used in digital elections.

API

Randomblind issuance is enabled in the scheme by adding the randomblind XML attribute to an Attribute tag within the issue specification of a given credential. For more information about schemes, see this page. In the example below we enable this for the second attribute in the credential. Any or all atributes in a credential type can be randomblind.

<IssueSpecification version="4">
  ...
  <Attributes>
    <Attribute id="...">
      ...
    </Attribute>
    <Attribute id="..." randomblind="true">
      ...
    </Attribute>
  ...
  </Attributes>
...
</IssueSpecification>

When issuing a credential specified by the above, the issuing party, i.e., the requestor that submits the issuance request to the IRMA server, must not pass attribute values for attributes that are tagged as randomblind. Instead, the issuer and user jointly decide on the value of these attributes (in this case the votingnumber attribute) during the session. We explain in detail how this comes to pass in the next section.

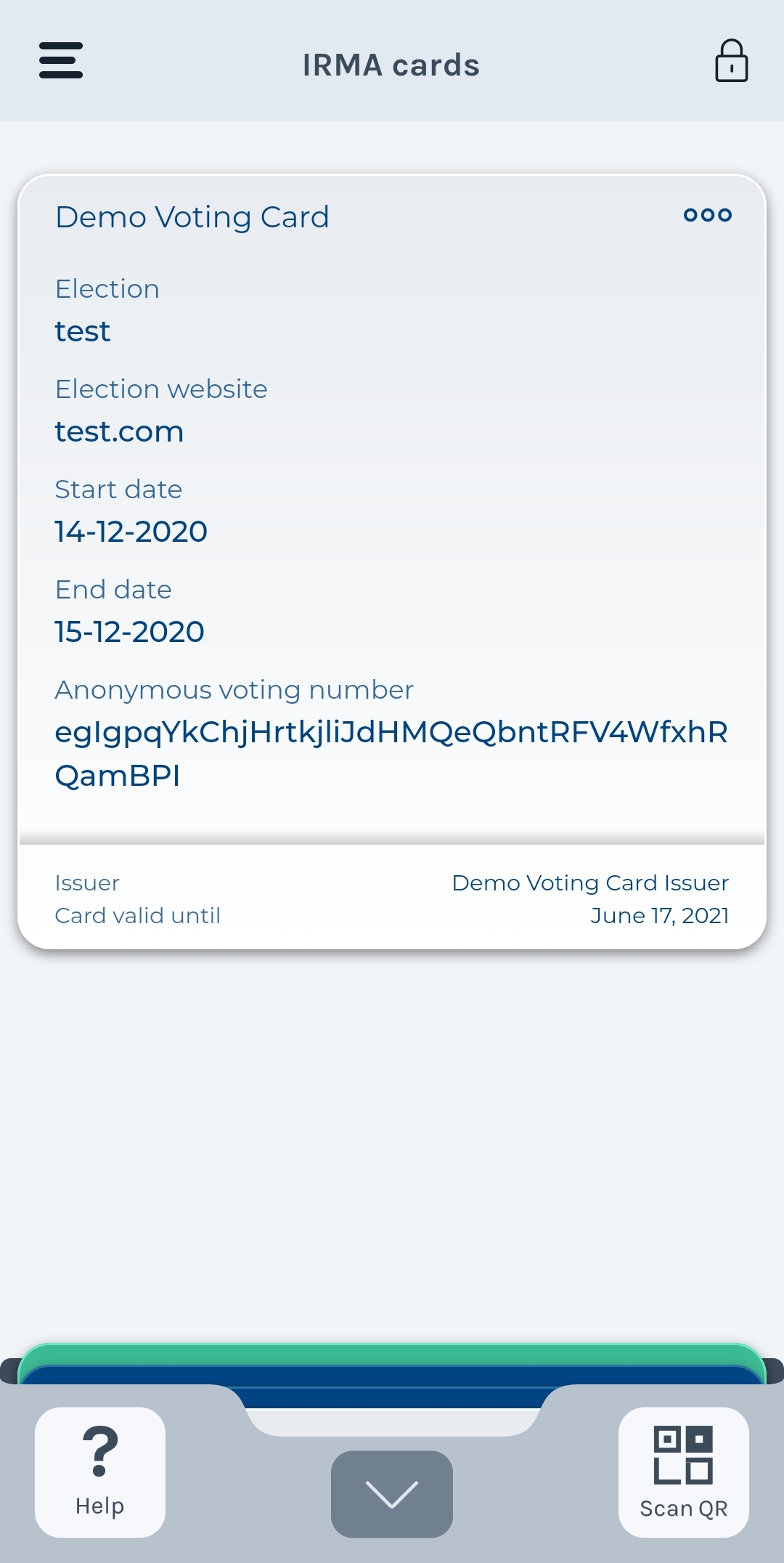
As a concrete example we use the "Demo Voting Card" credential type, see this page in the attribute index. Even though the credential contains five attributes, the issuer must only give four concrete values to construct the credential. For example, a requestor can start an issuance session to issue such a credential using the following command:

irma session --issue irma-demo.stemmen.stempas=test,test.com,14-12-2020,15-12-2020

Upon scanning the QR code, the Yivi app user is asked permission to perform the session and obtain this credential. At this point, the value of votingnumber has not been decided yet. After the issuance, a fifth attribute, votingnumber, which is at most 256 bits, shows up in the credential. The app displays this attribute in a base62 representation.

Before issuance	After issuance

Cryptography

In this section we will explain in detail how the issuer and the user are able to perform such an issuance session. Randomblindness of attributes only concerns the issuance protocol. The disclosure and signature protocols involving randomblind attributes are in every aspect identical to disclosing or signing using a normal attribute.

We can assume that the schemes of both parties agree on the indices of the randomblind attributes. If this is not the case, either party cancels the session. In the following example, we only have one randomblind attribute, but the protocol can be extended straightforwardly to issue multiple randomblind attributes.

The following requires a bit of background regarding Camenisch-Lysyanskaya (CL) signatures. A short summary can be found here. A more extensive description of the Idemix specification can be found here.

In the following, the variables $R, S$ and $Z$ are public parameters defined by the Idemix public key of the issuer. The issuance goes as follows:

• The user starts by sampling a random $v'$ and a random 255-bit integer $m_{r}'$ at the index $r$ of the randomblind attribute. This so-called share of the attribute remains secret, similar to how the user's secret key remains secret during issuance. The user computes the commitment $U = S^{v'} R_0^{m_0} R_r^{m_{r}'} \mod n$. Note that $m_0$ is always the user's secret key. This commitment is sent to the issuer along with a zero-knowledge proof of $v', m_0$ and $m_{r}'$.

• The issuer samples a random prime $e$. The issuer also samples $v''$ and $m_{r}''$ (also 255 bits) at random. Next, the issuer computes

  $$ A = \Bigg(\frac{Z}{U S^{v''} R_{1}^{m_1} \dots \ R_{r}^{m_r''} \dots \ R_{n}^{m_n}}\Bigg)^{1/e} $$

  For every attribute that is tagged randomblind, the issuer includes its share of the attribute in the exponent (in this case, only for index $r$). For regular attributes, the exponent is simply the attribute value that the issuer wants to pass. The issuer sends $(A, e, v'', m_{r}'')$ back to the user.

• Finally, the user is able to reconstruct any attributes that are the sum of two shares: $$ m_r = m_r' + m_r'' $$

  The CL signature becomes $(A, e, v)$ with $v = v' + v''$. It follows that $Z = A^e S^v \prod_{i=0}^{l} R_{i}^{m_i}$ holds for the attributes $m$ in the resulting credential, meaning that the signature (and thereby the credential) is valid. We also note that the issuer does not have enough information to fully uncover $m_r$, which ends up as the attribute value in the resulting credential. The user is now free to use this attribute, knowing the issuer cannot trace it back to her. Note that after revealing this attribute once, this guarantee no longer holds.

Use case: Digital elections

Two important requirements in digital elections in not just an online setting, but rather in general, are secrecy and verifiability. Secrecy means that nobody else is able to figure whom someone voted for. Verifiability means that any user of the system is able to verify that her vote is included in the final tally. In this section we explain how IRMA's randomblind attributes can help realize these requirements.

A key observation to preserve secrecy is that there has to be a split between authenticating the user and registering the votes. In physically held elections this is realized by handing out an anonymized ballot after the user has proven eligibility. For this purpose, two parties are required; one that the user authenticates to after which this party determines if the user is eligible (party A); and one that registers votes (party B). It is crucial that these parties are strictly separate and do not conspire together.

In digital elections, the same principle applies. Using IRMA randomblind attributes the following system can be realized:

1. (Eligibility check & voting pass retrieval). The user authenticates to party A (perhaps using IRMA), which then decides whether or not this user is eligible as per the system's criteria. In this process, party A learns (part of) the identity of the user. If the user is eligible, the party issues a voting card, which includes a randomblind attribute. Since party A does not learn the value of the attribute, this party can also not learn whom or what a user decides to vote for in the upcoming steps. Note that in order to prevent a user from fetching more than one voting card (and thus being able to cast multiple votes), the user must be uniquely identified in this stage.

2. (Casting the vote). To vote, a user creates an attribute-based signature on a "ballot" string, i.e., the user's choice using the randomblind attribute acquired in the previous step. This signature, the choice and the attribute are then registered in a database at party B. The signature ensures authentication, integrity and non-repudiation. Note that party B only learns what somebody voted for, but not the actual identity of the voter.

3. (Verification). After the election ends, the database is published. To verify whether her vote has been correctly cast, the user can simply check if the attribute-based signature created in the previous step containing her randomblind attribute is among the registered vote entries.